La sécurité des transactions

Bases de cryptographie

Les services fournis

Historiquement, la cryptographie est l'étude des méthodes permettant de transmettre des données de manière confidentielle :

le chiffrement (parfois aussi appelé cryptage) des données consiste à appliquer à un texte clair une transformation qui le rend incompréhensible
inversement le déchiffrement consiste à restituer le texte clair à partir des données chiffrées.

Les transformations appliquées pour chiffrer ou déchiffrer un message sont des fonctions mathématiques dépendant d'un paramètre appelé la clé.
Le décryptage est l'activité consistant à retrouver le texte clair sans connaître la clé.

De nos jours, le but de la crytographie n'est plus seulement la confidentialité des transmissions mais de fournir un certain nombre de services parmi lesquels :

la confidentialité : transmettre sans qu'un tiers ne puisse avoir connaissance de la teneur du message
l'intégrité : s'assurer que le message reçu est bien conforme au message expédié
l'authentification de l'origine des données : s'assurer que l'expéditeur du message reçu n'est pas un tiers mal intentionné
la non-répudiation : fournit à l'expéditeur l'assurance que le message transmis ne pourra pas être modifié par le destinataire mal intentionné

Les techniques employées

Le chiffrement est à la base des services de confidentialité.

Pour le reste, on emploie des méthodes de scellement et de signature ainsi que des protocoles d'authentification mutuelle avec échange de clef.

La confidentialité des données

Rappelons que la confidentialité consiste à transmettre un message sans qu'un tiers ne puisse avoir connaissance de sa teneur.

C'est historiquement le service le plus ancien fourni par la cryptographie.

Les techniques employées sont les algorithmes de cryptage à base de clés.

Il existe deux grandes familles de tels algorithmes :

les algorithmes à clé secrète ou algorithmes symétriques
les algorithmes à clé publique ou algorithmes asymétriques

Le chiffrement symétrique

Le principe

La clé doit être tenu secrète : elle sert aussi bien à chiffrer qu'à déchiffrer le message.

Déroulement des opérations :

L'expéditeur chiffre le message clair avec la clé secrète.
Le message chiffré incompréhensible résultant est transmis au destinataire.
Celui-ci déchiffre le message avec la même clé secrète.

Les algorithmes à clé secrète

Ils se partagent en deux familles :

Les algorithmes de chiffrement en continu

Aussi appelés stream cipher, ils agissent sur un bit à la fois sans attendre la réception complète des données à crypter.
Les stream-ciphers sont utilisés aujourd'hui par différentes applications. Pour chiffrer les flux, l'algorithme RC4 est très utilisé.

Les algorithmes de chiffrement par blocs

Aussi appelés block cipher, ils agissent sur un bloc de données de taille fixe (généralement 64 bits).

Les plus célèbres sont

DES : (clé de 56 bits)
3DES : 3 clés distinctes (EDE)

Quatre modes de chiffrement par bloc sont utilisés : Electronic CodeBook (ECB), Cipher Block Chaining (CBC), Cipher FeedBack (CFB) ou Output FeedBack (OFB).

le mode Electronic CodeBook (ECB) consiste à chiffrer chaque bloc complètement indépendanmment des autres
dans le mode Cipher Block Chaining (CBC), le résultat du chiffrement de chaque bloc est utilisé pour chiffrer le bloc suivant
le mode Cipher FeedBack (CFB) peut être considéré comme un intermédiaire entre un cryptage par blocs et un cryptage en continu. En effet, il permet de crypter des blocs dont la longueur peut varier de n à 1 bits/blocs. Sachant que dans ce dernier cas, il serait plus économique en calculs d'utiliser directement un algorithme en continu.
Le mode Output FeedBack (OFB) est une variante de mode CFB. Il présente beaucoup de problèmes de sécurité et il est peu conseillé.

Problème de l'échange des clés

Il faut disposer d'un canal de communication sûr pour pouvoir échanger les clés secrètes.

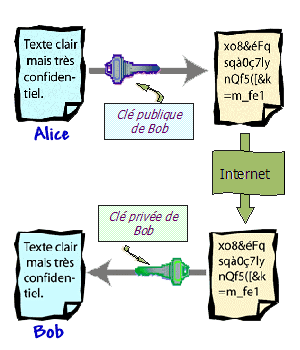
Le chiffrement asymétrique

Le principe

Ils sont basés sur des problèmes difficiles à résoudre tels que la factorisation de grands nombres.

Les clés de chiffrement et de déchiffrement sont distinctes. L'une est privée (secrète), l'autre est publique.La connaissance de la clé publique ne permet pas de découvrir la clef secrète.

Déroulement des opérations :

L'expéditeur chiffre le message clair avec la clé publique.
Le message chiffré incompréhensible résultant est transmis au destinataire.
Celui-ci déchiffre le message avec la clé privée qu'il est seul à posséder.

Étant donné que tous les algorithmes à clé publique sont bien plus lents que les algorithmes à clé secrète, on se contente généralement de les utiliser pour transmettre au destinataire la clé secrète d'un algorithme à clé secrète, le reste du message étant alors chiffré avec cet algorithme plus rapide.

Les algorithmes à clé publique

Le plus célèbre est RSA du nom de ses inventeurs (Rivest, Shamir et Adelman en 1977).

Le principe en est le suivant :

On choisit p et q deux grands nombres premiers
On calcule n = p·q
On calcule aussi φ(n) = (p-1)·(q-1)
On choisit un entier e qui soit premier avec (p-1) et (q-1), et donc avec φ(n)
On calcule à l'aide de l'algorithme d'Euclide un entier d tel que e·d = 1 modulo φ(n)
- le couple (n,e) représente la clé publique
- d représente la clé privée
Soit M le message clair à transmettre. Le message chiffré correspondant est :
C = Me modulo n
Le destinataire déchiffre en calculant Cd modulo n, c'est-à-dire Med modulo n ou encore M1 modulo n puisque ed = 1 modulo φ(n).

Remarques :

La valeur φ(n) est en fait le nombre d'entiers inférieurs à n qui sont premiers avec lui. La fonction φ est appelée fonction indicatrice d'Euler.
L'existence du nombre d est assurée grâce au théorème de Bezout : pour trouver sa valeur, il faut chercher le plus petit m>0 tel que m·φ(n)+1soit divisible par e.
Une fois la valeur de m déterminée, on obtient d en divisant m·φ(n)+1par e.
NB. Ceci est une méthode utilisable "à la main". Dans la pratique, on utilise l'algorithme d'Euclide étendu pour déterminer d.

Exemple :

Choisissons p = 31 et q = 23 (dans la réalité, p et q sont beaucoup plus grands)
On obtient n = 713
On calcule φ(n) = 660
Choisissons e = 7, premier avec 30 et 22, donc avec 660
On calcule la clé secrète : le nombre 3x660+1 est divisible par 7, le quotient vaut 283.
Ceci sera la clé secrète de déchiffrement
Soit à coder le nombre 10 : le reste de la division de 107 par 713 vaut 175.
La valeur chiffrée est donc 175.
En élevant 175 à la puissance 283 et en prenant le reste de la division par 713, on obtient à nouveau 10.

Jouons : dans le formulaire ci-dessous, choisir les entiers p et q, l'entier e et la valeur du message à coder.

Chiffrement mixte

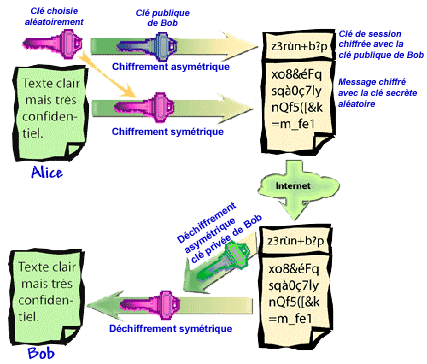
Le chiffrement mixte se définit par l'utilisation conjointe d'algorithmes symétriques et asymétriques pour chiffrer des données.

Le chiffrement asymétrique est utilisé pour chiffrer une clé de session, choisie aléatoirement par l'expéditeur.

Le message lui-même est chiffré avec cette clé de session à l'aide d'un algorithme de chiffrement symétrique.

Le principe détaillé est le suivant :

l'expéditeur chiffre le message avec une clé secrète d'un algorithme de chiffrement symétrique
il chiffre également la clé secrète avec la clé publique du destinataire en utilisant un algorithme de chiffrement asymétrique
Il transmet le message crypté en 1 et la clé secrète cryptée en 2
le destinataire déchiffre la clé secrète avec sa clé privée
il l'utilise alors pour déchiffrer le message reçu

L'authentification et l'intégrité

Il s'agit ici d'être capable de s’assurer que le message reçu

émane bien de l’expéditeur annoncé (c'est l'authentification de l’origine des données)
n’a pas été modifié pendant le transfert (c'est l'intégrité)

Authentification

La manière la plus classique d'assurer l'authentification consiste à utiliser un algorithme de cryptage asymétrique en inversant le rôle des clés publiques et privées.

L'expéditeur ayant chiffré son message avec sa clé privée (qu'il est donc seul à connaître), tout un chacun possédant la clé publique correspondante peut déchiffrer le message et ainsi être assuré de son origine.

Remarque :

en général, cette méthode est peu utilisée du fait de sa lenteur. En pratique, on ne chiffre pas le message en entier, mais uniquement une empreinte calculée à partir du message par une fonction de condensation ou fonction de hachage à sens unique (voir ci-dessous).

Intégrité

Pour vérifier l'intégrité du meessage transmis, il est possible d'utiliser la technique des empreintes ("hash" ou "checksum", ou "message digest") : une empreinte caractéristique du message est calculée à partir du message à transmettre. Elle est transmise par un canal sûr en même temps que le message : le destinataire pourra alors recalculer l'empreinte du message reçu et la comparer avec l'empreinte qui lui a été transmise : si les deux empreintes sont différentes, le message a été altéré au cours de la transmission.

Remarque :

la transmission de l'empreinte nécessite à la fois un canal sûr et authentifié. Sinon, un tiers pourrait l'intercepter, modifier le message, recalculer l'empreinte et la transmettre avec le message modifié, faisant croire au destinataire à l'intégrité du message. Authenticification et intégrité sont donc inséparables : on emploie souvent le terme authenticité pour désigner l'ensemble authenticification + intégrité.

Les fonctions de hachage

Le principe

Une fonction de hachage convertit une chaîne de longueur quelconque en une chaîne de taille inférieure, généralement fixe, appelée empreinte.

Pour être sûres, les fonctions de hachage doivent avoir certaines propriétés :

elle doivent à sens unique : il doit être très difficile de reconstituer le message à partir de son empreinte ou même d'engendrer une chaîne qui ait une empreinte donnée.
elles doivent être sans collision : il doit être très difficile de trouver deux textes différents qui aient la même empreinte, ce qui suppose que la modification du moindre bit dans le texte initial entraîne le changement de valeur de l'empreinte.

Les fonctions de hachage sont en général obtenues par itération d'une compression : le message M est décomposé en blocs. Puis une fonction de compression est appliquée à chaque bloc et au résultat de la compresion du bloc précédent : le résultat de la fonction de hachage est le résultat de la dernière compression.

Les algorithmes de hachage

MD2, MD4 : ce sont d'anciennes fonctions de condensation de RSA Data Security, il existe des faiblesses connues et leur utilisation n'est pas recommandée.
MD5 (Message Digest Algorithm 5) : développé par RSA Data Security, renvoie une chaîne de 128 bits. Des faiblesses ont été trouvées...et son utilisation se raréfie.
SHA-1 (Secure Hash Algorithm) : algorithme de condensation publié par le gouvernement US. L'un des plus utilisé avec MD5. Il renvoie une valeur de 160 bits. Il est relativement jeune, et il n'y a pas de faiblesse connue.
SHA-2 : agrandit la taille de l'empreinte.
RIPEMD-160 : a été conçu pour remplacer MD4 et MD5 ; renvoie une valeur de 160 bits.
SHS (Secure Hash Standard) : successeur de SHA-1 et SHA-2.

Le scellement

Sceller un message consiste à lui apposer un sceau garantissant son authenticité (authentification + intégrité).

Principe

Un MAC (Message Authentication Code) est une empreinte calculée à partir du message par une fonction de hachage à sens unique indexée par une clef secrète : on ne se contente pas de calculer l'empreinte du message, mais on y ajoute une clé secrète connue seulement de l'expéditeur et du destinataire.

Le re-calcul de l'empreinte d'un message modifié par un tiers mal intentionné n'est donc plus possible.

Par contre, dans la mesure où le destinataire partage le secret de la clé avec l'expéditeur, un correspondant mal intentionné pourra modifier le message, recalculer son MAC et prétendre avoir reçu ou expédié ce message modifié : c'est ce que l'on appelle la répudiation.

Le scellement n'offre pas le service de non-répudiation : il faudra utiliser pour cela des techniques de signature électronique.

Techniques utilisées

DES-MAC

Le DES-MAC consiste à chiffrer le message avec DES en mode CBC et à utiliser comme MAC le dernier bloc du cryptogramme ainsi obtenu.

Keyed-MAC

Une autre technique consiste à faire opérer une fonction de hachage classique tel que MD5 ou SHA-1 sur le message auquel on a rajouté des données secrètes : le MAC est généralement le résultat de H(secret, message, secret).

Exemples : Keyed-MD5, Keyed-SHA-1

HMAC

HMAC est une technique plus élaborée et plus sûre que Keyed-MAC. Elle peut être utilisée avec n'importe quelle fonction de hachage itérative telle que MD5, SHA-1 ou RIPE-MD.

Elle consiste à calculer H(Ko, H(Ki,M)) où Ki et Ko sont obtenus en appliquant un Ou exclusif à la clé secrète et à une chaîne constituée du caractère 0x36 pour Ki et 0x5C pour Ko.

Une pratique courante consiste à tronquer la sortie pour ne garder comme MAC qu’un nombre réduit de bits.
Exemple : HMAC-SHA-1-96 calcule une empreinte de 160 bits tronqué à 96.

La signature numérique

La norme ISO 7498-2 définit la signature numérique comme "des données ajoutées à une unité de données, ou transformation cryptographique d'une unité de données, permettant à un destinataire de prouver la source et l'intégrité de l'unité de données et protégeant contre la contrefaçon (par le destinataire par exemple)". La mention "protégeant contre la contrefaçon" signifie que seul l'expéditeur doit être capable de générer la signature.

Une signature numérique fournit donc tout à la fois les services d'authentification, d'intégrité et de non-répudiation

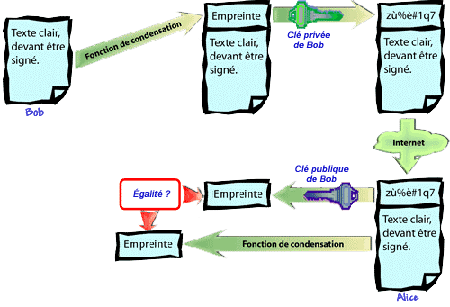
Le principe

Il consiste à chiffrer l'empreinte à l'aide de la clé privée d'un algorithme asymétrique.

L'empreinte ainsi signée est transmise en même temps que le message en clair : pour s'assurer que les données n'ont pas été modifiées, le destinataire recalcule l'empreinte des données. Puis il déchiffre l'empreinte qui accompagnait les données lorsqu'il les a reçues grâce à la clé publique de l'expéditeur (qui est en général jointe aux données signées).
Il compare ensuite ces deux résultats :

s'ils sont différents, cela signifie que les données ont été modifiées ou que la clé privée utilisée pour signer ne correspond pas à la clé publique utilisée pour vérifier.
si les résultats sont égaux, outre la garantie d'intégrité, il sera assuré du fait que les données ont été signées avec la clé privée associée à la clé publique qu'il a utilisée pour déchiffrer l'empreinte.

Remarques :

le destinataire ne pourra être assuré de l'identité du signataire que si sa clé publique était encapsulée dans un certificat (qui associe de façon certaine un identifiant à une clé publique), ou bien qu'un lien de confiance direct lui permet de considérer la clé publique comme appartenant à telle personne
dans le cas ou le signataire est le seul à posséder sa clé privée, et seulement dans ce cas, la signature électronique assure la non-répudiation car le signataire ne peut nier avoir fait cette opération si elle a été faite.

Algorithmes

Un algorithme de signature numérique est simplement l'association d'une fonction de hachage à sens unique et d'un algorithme de cryptage asymérique.

On utilise en général MD5 + RSA ou SHA-1 + RSA.

Echange de valeurs publiques

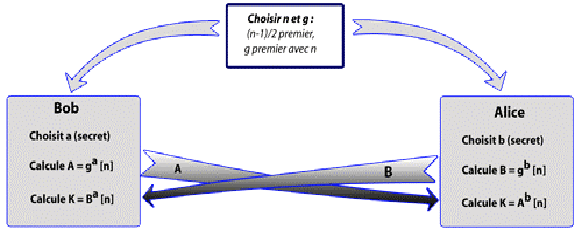
L'échange de valeurs publiques permet à deux tiers de générer un secret partagé sans disposer d'aucune information préalable l'un sur l'autre.Le secret généré peut ensuite être utilisé pour dériver une ou plusieurs clés secrètes (clefs de chiffrement symétrique par exemple).

L'algorithme de Diffie-Hellman met en oeuvre l'échange de valeurs publiques entre deux protagonistes P1 et P2. Le principe en est le suivant :

on choisit un nombre entier n tel que (n-1)/2 soit premier et un nombre g premier avec n. Ces deux valeurs sont publiques.
P1 choisit un grand nombre entier a qui constituera sa clé privée. Il calcule la clé publique correspondante :
A = ga mod n
P2 choisit un grand nombre entier b qui constituera sa clé privée. Il calcule la clé publique correspondante :
B = gb mod n
P1 et P2 échangent alors leurs clés publiques
Recevant B, P1 l'élève à la puissance a modulo n et obtient K = gab mod n
Recevant A, P2 l'élève à la puissance b modulo n et obtient aussi K = gab mod n

Un tiers qui intercepterait la communication connaîtrait n, g, A et B, ce qui ne lui permet pas de déduire facilement K.

Le point faible de l'algorithme réside dans l'échange des clés publiques : un tiers mal intentionné peut intercepter la communication et envoyer ses propres clés publiques à la fois à P1 et P2.

L'algorithme de Diffie-Hellman authentifié consiste à authentifier les clés publiques lors de leur échange. En règle général, cette authentification se fait par l'emploi de certificats.

Certificats

Un certificat est une carte d'identité numérique possédant une durée de vie limitée et attestant qu'une clé publique appartient à une entité particulière.

Plus précisement, le rôle du certificat est d'associer de facon non équivoque une clé publique avec une entité.

Attester de la validité d'une clé publique

Lorsque l'on recoit un message signé d'une entité E, le certificat permet de vérifier que le message a bien été émis par E. La vérification de la signature avec la clé publique de E (KpE) ne permet pas d'affirmer que c'est bien E qui a envoyé le message. Il faut en effet vérifier que KpE est bien la clé publique de E. C'est le rôle du certificat X509.

Un tel certificat est émis par une autorité de confiance (Certification Authority, CA en anglais) pour attester que la clé publique qu'il contient est bien la clé publique de l'entité désignée dans le certificat.

Pour cela, le certificat doit être signé par l'entité CA. Cette entité possède elle-même un certificat signé par une autorité supérieure. Les autorités de certification (CA) sont organisées en structure d'arbre. Au sommet de la hiérarchie se trouve le root qui signe lui-même son certificat.

Composition d'un certificat

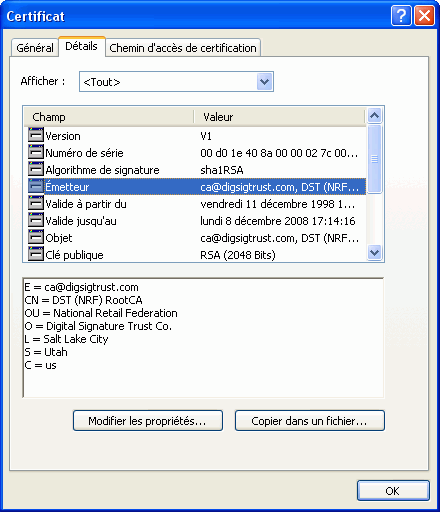
Certificat X509

Un certificat comporte principalement les informations suivantes :

Version : version du certificat (1, 2 ou 3 pour X509v1, X509v2 ou X509v3)
Serial number : identifiant unique d'un certificat
Signature Algorithm Id : description de l'algorithme de signature de l'autorité de certification.
Issuer Name : nom de l'autorité de certification qui a généré le certificat (sous la forme d'un Distinguished Name)
Validity period : période de validité du certificat.
Au-delà de ces dates, on parle d'expiration du certificat.
En cas de suspension de validité durant cette période, on parle de révocation.
Subject Name : nom de l'utilisateur auquel appartient le certificat (sous la forme d'un Distinguished Name)
Subject public key info : description de l'algorithme + valeur de la clé publique de l'utilisateur auquel appartient le certificat
Issuer Unique Id/ Subject Unique Id : extensions optionnelles introduites avec la version 2 de X509
Extensions : extensions optionnelles introduites avec la version 3 de X509
Signature : signature de l'autorité de certification CA.

Les extensions de la version 2

La version 2 du standard X509 a introduit les deux champs optionnels suivants :

Authority Key Identifier : ce champ identifie de façon unique la paire de clé utilisée par l'émetteur de certificats pour signer le certificat. Il peut être utilisé par une application pour faciliter le processus de vérification de la signature du certificat dans le cas ou l'AC a utilisé plusieurs clés depuis sa mise en service.
Subject Key Identifier : ce champ identifie de façon unique la paire de clé dont la clé publique est contenue dans le certificat. Il peut être utile si l'utilisateur possède un historique de clés (c'est à dire que ses clés ont été renouvelées une ou plusieurs fois). Par exemple, pour déchiffrer un document chiffré avec une clé qui n'est plus celle en cours de validité, ce champ permet de retrouver rapidement la bonne clé privée.

Les extensions de la version 3

Les extensions qui sont apparues dans la version 3 du standard X509, peuvent être classées en 4 catégories :

complément d'informations sur la clé
complément d'informations sur l'utilisation du certificat
complément d'informations sur l'utilisateur et les CA
informations sur la co-certification

Informations sur la clé

Elles renseignent sur l'utilisation qui doit être faite de la clé publique et du certificat

Key usage : ce champ renseigne sur l'utilisation qui doit être faite de la clé. Si le champ criticality de cette extension est à TRUE, alors la clé ne doit être utilisée que dans le but spécifié, et toute autre utilisation serait contrevenir à la politique de l'AC ou de la PKI. Si le champ criticality de cette extension est à FALSE, alors le champ Key usage est là à titre indicatif pour faciliter les processus par exemple.
Les valeurs possibles sont : digitalSignature, nonRepudiation, keyEncipherment, dataEncipherment, keyAgreement, keyCertSign, cRLSign, encipherOnly, decipherOnly.
Private Key Usage Period : ce champ donne la date d'expiration de la clé privée associée à la clé publique contenue dans le certificat. Il est en général utilisé pour les clés privées de signature (et donc contenu dans les certificats de signature dans le cas ou ils sont distincts de ceux de chiffrement), qui peuvent expirer, ce qui n'est pas le cas des clés privées de déchiffrement (il doit toujours être possible de déchiffrer des données, même si celles-ci ont été chiffrées avec une clé publique qui est maintenant expirée).

Informations sur l'utilisation du certificat

Ce groupe d'extensions, qui contient deux champs, permet à un émetteur de certificats de spécifier les façons dont un certificat doit être utilisé, en accord avec la politique qu'il a définie (PC). Les deux champs sont : Certificate Policies et Policy Mappings.

Certificate Policies : ce champ peut donner, soit la politique de certification qui a présidé à l'émission du certificat, soit les utilisations qui doivent être faites du certificat. Il peut spécifier ces deux informations à la fois.
Les politiques de certificats sont représentées par des Object Identifier (OID), qui sont des séries de nombres séparées par des points. Ces OID sont enregistrées au niveau international, et leur utilisation est standardisée. Un certificat peut contenir plusieurs OID, pourvu qu'elles ne soient pas incompatibles.
Si ce champ est marqué comme étant critique, l'émetteur de certificats impose que le certificat soit utilisé conformément à la politique de certification. Dans le cas contraire, l'information est indicative ("ce certificat devrait être utilisé dans tel but" par exemple)... Libre à l'application cliente (son implémentation ou sa configuration) de respecter ou pas la criticité.
Policy Mappings : ce champ ne concerne que les co-certificats (le certificat émis par une AC pour certifier la clé publique (le certificat) d'une autre AC). Il permet d'associer la politique de certification de l'AC qui émet le certificat à la politique de certification indiquée dans le co-certificat. S'il est défini comme critique, il permet aux applications qui vérifient un certificat appartenant à une chaîne de certification de s'assurer qu'une politique de certification acceptable s'applique à tous les certificats.

Attributs des utilisateurs et des AC

Ce groupe d'extensions permet de mieux spécifier l'identification des utilisateurs et des certificats.

Subject Alternative Name : ce champ spécifie un ou plusieurs noms uniques et supplémentaires pour le détenteur du certificat. Ils peuvent être utilisés dans les applications de messagerie, web, réseau où il peut être très utile d'identifier un utilisateur, ou une machine, autrement que par un DN. Les noms autorisés sont : une adresse mail, un nom de domaine, une adresse IP, une adresse mail X.400, un nom EDI, une URL, un nom défini par une OID
Issuer Alternative Name : ce champ permet de donner un nom spécifique à une AC, et les noms autorisés sont les mêmes que ceux du champ précédent.

Contraintes sur la co-certification

Les trois extensions de ce groupe permettent de limiter et contrôler la confiance envers d'autres AC en cas de co-certification.

Basic Constraints : ce champ indique si l'utilisateur est un utilisateur final ou s'il peut être une AC. S'il peut être AC, le certificat est alors un co-certificat. On définit alors une "distance de certification". Elle spécifie jusqu'où doit remonter une application qui veut vérifier un certificat en consultant sa CRL, et jusqu'ou est étendue la confiance dans la chaîne. Si cette distance est par exemple à 1, les utilisateurs ne peuvent que vérifier les certificats émis par l'AC défini dans le co-certificat.
Name Constraints : ce champ n'est utilisé que dans les co-certificats, et permet aux administrateurs de restreindre les domaines de confiance dans un domaine de co-certification.
Policy Constraints : ce champ s'applique aux co-certificats, et permet de spécifier les politiques de certification acceptables pour les certificats dépendants du co-certificat.

Le fonctionnement détaillé

Supposons qu'une société X veuille faire du commerce en ligne : pour des raisons de sécurité évidentes, les numéros de carte bancaire de ses clients devront au moment du paiement être chiffrés afin d'empêcher leur interception par un tiers.

La société X va donc faire parvenir à son client sa clé publique PKX.

Pour que le client soit certain que cette clé publique est bien celle de la socité X, cette clé PKX va être englobée dans un certificat émis par exemple par l'autorité de certification Y.

Nous supposons que le client dispose déjà de la clé publique PKY de l'autorité de certification Y et qu'il a confiance dans cette clé.

Que contient exactement le certificat de la société X ?

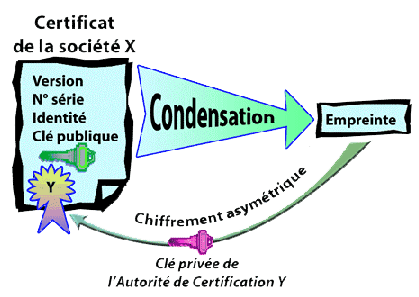
Le certificat de la société X peut être décomposé en deux sous-ensembles distincts :

le certificat CX proprement dit
la signature apposée à sa suite par l'autorité de certification Y.

Cette signature est composée de l'empreinte de CX (calculée avec un algorithme précisée dans le certificat) chiffrée ensuite avec la clé secrète SKY de l'autorité de certification CA.

Signature = chiffrement_asymétrique(SKY, Empreinte(CX))

Comment vérifier la validité de la clé publique ?

Pour vérifier la validité de la clé publique contenue dans le certificat de la société X, le client va

Déchiffrer cette signature avec la clé publique PKY de l'autorité de certification Y (supposée en sa possession). Le résultat est donc l'empreinte du certificat CX.
Re-calculer lui-même cette empreinte (avec l'algorithme spécifié) à partir du certificat CX qui lui a été communiqué.

Si ces deux empreintes sont identiques, alors le client a l'assurance (fournie par l'autorité de certification Y) de l'authenticité du certificat CX.

Il peut donc raisonnablement utiliser la clé publique PKX contenue dans CX pour chiffrer les données transmises lors du paiement par exemple.

À l'autre bout, la société X utilisera sa clé secrète SKX pour déchiffrer ce message.

Quid de la confiance dans le CA ?

Dans le processus décrit ci-dessus, le client est censé avoir confiance dans la clé publique de l'AC.

En pratique, les applications telles que les navigateurs disposent d'un certain nombre de clés publiques de telles autorités de confiance (plus d'une centaine dans IE !).

Certificat IE

Si ce n'est pas le cas, il est toujours possible de ré-appliquer ce même processus pour vérifier l'authenticité de la clé publique de l'AC à partir de la clé publique de l'autorité de confiance qui a signé le certificat de l'AC.

Évidemment, parvenu à la racine de l'arbre, on arrive à un certificat auto-signé, émis par une autorité en qui il faudra bien avoir confiance...

Législation

En France, la loi du 13 mars 2000 sur la valeur de la preuve dans les documents électroniques confère à la signature numérique le même pouvoir de preuve qu'une signature écrite.

Autres textes :

Décret du 30 mars 2001 : Définition de la signature présumée fiable (signature électronique sécurisée)
Décret du 18 avril 2002 : Description du processus de certification des produits et systèmes
Arrêté du 31 mai 2002 : Description du processus de qualification des prestataires de service de certification

Voir aussi :